Siły oporu
działają na nas nieustannie, począwszy od oporu powietrza po siły oporu tarcia
zwane po prostu siłą tarcia.
Charakterystyczną cechą sił oporu jest to, że wraz z rosnącą siłą rośnie siła reakcji – czyli siła oporu właśnie. Siłą
oporu to również reakcja podłoża na nacisk zewnętrzny. Im większą siłę
przykładamy tym siła reakcji jest większa, zgodnie z III Zasadą Dynamiki Newtona. Nieustannie zwiększając nacisk na
dany materiał, dojdziemy do punktu w którym teoretycznie siła reakcji będzie
mniejsza od siły nacisku, co spowoduje złamanie, ukruszenie materiału lub inne
odkształcenie.
Ciekawostka
Zazwyczaj w zadaniach pomijamy opór powietrza podczas opisu ruchu spadającego przedmiotu. Uznajemy wtedy, że jedyną siłą działającą na ciało jest przyciąganie ziemskie, które nadaje przedmiotowi przyśpieszenie, zatem przedmiot porusza się ruchem jednostajnie przyśpieszonym. W rzeczywistości jednak tak nie jest! Ciało na początku rzeczywiście porusza się ruchem jednostajnie przyśpieszonym, jednak wraz ze wzrostem prędkości (który jest bardzo szybki, gdyż przyśpieszenie ziemskie  ). Rośnie siła oporu, która w pewnym momencie staje się równa sile przyciągania ziemskiego, a więc działające na ciało siły równoważą się - zgodnie z I zasadą dynamiki Newtona ciało to porusza się ruchem jednostajnym.
). Rośnie siła oporu, która w pewnym momencie staje się równa sile przyciągania ziemskiego, a więc działające na ciało siły równoważą się - zgodnie z I zasadą dynamiki Newtona ciało to porusza się ruchem jednostajnym.
 ). Rośnie siła oporu, która w pewnym momencie staje się równa sile przyciągania ziemskiego, a więc działające na ciało siły równoważą się - zgodnie z I zasadą dynamiki Newtona ciało to porusza się ruchem jednostajnym.
). Rośnie siła oporu, która w pewnym momencie staje się równa sile przyciągania ziemskiego, a więc działające na ciało siły równoważą się - zgodnie z I zasadą dynamiki Newtona ciało to porusza się ruchem jednostajnym. Tarcie Statyczne a Dynamiczne
Występowanie siły tarcia jest reakcją podłoża na nacisk jaki wywołujemy na nim czyli na siłę jaką działamy na podłoże (może być również spowodowany składową sił działających na ciało, nie koniecznie specjalnie). Zauważmy, że gdy próbujemy przesunąć coś bardzo ciężkiego jak np. szafa mimo, że działamy pewną siłą szafa nie przesuwa się. Jest to spowodowane tarciem statycznym, które występuje podczas braku ruchu. Wraz ze wzrostem przykładanej siły rośnie tarcie statyczne, aż do momentu granicznego, gdy uda nam się wykonać pracę (spowodować przesunięcie) wtedy tarcie statyczne przeradza się w tarcie dynamiczne, czyli takie, które uwzględniamy w opisie poruszających się ciał.
Zadania z Równią Pochyłą
Na początku należy wyrysować układ kartezjański w nasze ciało. Robimy to w
środku ciała sprowadzając ciało do punktu (można rysować ciało lub punkt).
Rysujemy linię równoległą do pochyłości równi oraz prostopadła do niej. Linie
przerywane to nasz prowizoryczny układ współrzędnych.
Następnie rysujemy wszystkie (prócz pomijanych)
siły działające na to ciało. Na ciało ZAWSZE działa siła przyciągania
ziemskiego zwana siłą grawitacji ZAWSZE, bez względu na to gdzie się znajduje, pionowo w dół.
Jeżeli ciało znajduje się pod kątem, czyli jak
w przypadku ciała na równi pochyłej należy rozłożyć siłę na składowe, w tym
przypadku na siłę nacisku FN oraz siłę zsuwającą Fs.
Zgodnie z III zasadą dynamiki reakcją na siłę nacisku jest jakaś siła, którą
dla wygody nazwijmy siłą reakcji FR.
WAŻNE: Za ruch zawsze odpowiada siła
działająca równolegle do ruchu!!!
Następnie
należy uwzględnić siłę tarcia T (jeśli wymaga tego zadanie). Tarcie ZAWSZE
działa w przeciwnym kierunku do ruchu ciała. W naszym przypadku ciało zsuwa się
z równi zatem:
Z podobieństwa trójkątów oraz własności trygonometrycznych wynikają
poniższe wzory (które łatwo się wyprowadza, po wykonaniu poprawnego rysunku):
Empirycznie
każdy czuje, że im mocniej dociśniemy przedmiot do podłogi, tym trudniej będzie
nam go przesunąć, ergo siła tarcia działająca na to ciało będzie większa stąd:
Należy
zwrócić uwagę, że tarcie występuje nie tylko w ruchu po równi pochyłej, lecz
ogólnie w każdym rodzaju ruchu, gdy przedmiot ma kontakt z podłożem:
WAŻNE: Siła tarcia ZAWSZE działa przeciwnie do ruchu ciała
Należy
zwrócić uwagę, że tarcie występuje nie tylko w ruchu po równi pochyłej, lecz
ogólnie w każdym rodzaju ruchu, gdy przedmiot ma kontakt z podłożem:
Zadania:
Zad 1. Dane
jest masa klocka, kąt nachylenia równi i współczynnik tarcia. Ile wynosi
siła tarcia dla klocka w ruchu i spoczywającego?
Dane: m, α, f Szukane: T = ? Ts = ?
Na początku rozrysowujemy wszystkie siły działające na
nasze ciało na równi:
Aby obliczyć siłę
tarcia w ruchu musimy założyć, że Fs i T nie równoważą się, zatem spełniona
jest II zasada dynamiki.
Inaczej sprawa ma się w
przypadku ciała w spoczynku. Zgodnie z I
zasadą dynamiki, aby ciało pozostało w spoczynku to nie mogą na nie działać
żadne siły (ten przypadek odrzucamy) lub działające na nie siły muszą się równoważyć:
Zad 2. Jaki kąt
nachylenia powinna mieć równia o współczynniku tarcia f = 0,5, aby
klocek postawiony na niej nie zsuwał się?
Dane: f
= 0,5 [wartość bezwymiarowa] Szukane: α = ?
Jak w każdym zadaniu z
równią najpierw rozrysowujemy siły działające na ciało:
Zad 3. Z jaką siłą
należy ciągnąć ciało o masie 100 kg w górę gładkiej równi (gładka, czyli bez
tarcia!) o kącie nachylenia 30°? Ile razy mniej siły trzeba, aby wciągnąć
ten klocek po równi tej niż podnieć go?
Dane: m = 100 [kg] α = 30° T = 0 Szukane: F = ?
W zasadzie zadanie nie
jest precyzyjne. Siła jaką należy działać na ciało musi być większa od sumy sił
Fs i T zatem teoretycznie możemy podać dużą liczbę i to będzie poprawna
odpowiedź. Wg. I zasady dynamiki najmniejszą siłę jaką należy przyłożyć, aby
ciało poruszyło się musi równoważyć pozostałe siły. Dodatkowo zgodnie z tą
zasadą wiemy, że ciało będzie poruszać się wtedy ruchem jednostajnym.
Zad 4. Sanki zsuwają się ze szczytu toru o długości L pochylnego pod kątem do
poziomu, a następnie wjeżdżają na tor prosty. Wzdłuż całego toru działa na
sanki siła tarcia. Współczynnik tarcia na torze pochyłym wynosi f1 , zaś na
torze prostym f2. Oblicz jaką drogę s przebędą sanki po torze prostym.
Zad 5. Na klocek o masie 10 kg znajdujący się na poziomym podłożu, działa pozioma siła 100 N. Z jakim przyśpieszeniem poruszał się będzie klocek, jeżeli współczynnik tarcia o podłoże wynosi 0,2?
Zad 6. Jaką drogę przebędzie łyżwiarz, mający szybkość początkową wynoszącą 10 m/s do chwili zatrzymania, jeżeli współczynnik tarcia łyżew o lód wynosi 0,05.
Dane: V0 = 10 [m/s] f = 0,05
Szukane: s = ?
Zad 7. Oblicz współczynnik tarcia łyżew o lód, jeżeli szybkość łyżwiarza wynosi 10 m/s na drodze równej 25 m została zredukowana do 5 m/s.
Dane: V1 = 10 [m/s] V2 = 5 [m/s] s = 25 [m] Szukane: f = ?
Zad 8. Znajdź współczynnik tarcia kół samochodu o nawierzchnię szosy, jeżeli wiadomo, że przy szybkości samochodu 20 m/s droga hamowania wynosi 40 m.
Zad 9. Podnosząc stopniowo jeden koniec deski stwierdzono, że położony na niej klocek zaczął się zsuwać przy kącie nachylenia 30° . Oblicz współczynnik tarcia statycznego klocka o deskę.
Zad 10. Linia zaczęła zsuwać się ze stołu wtedy, gdy trzecia część jej długości była poza jego krawędzią. Oblicz współczynnik tarcia f.
Zad 11. Oblicz przyśpieszenie, z jakim zsuwał się będzie klocek z równi pochyłej o kącie nachylenia 30° z wysokości 1 m pod podstawą równi. Współczynnik tarcia jest równy 0,2. Jaką szybkość osiągnie ciało u podstaw równi?
Zad 12. Oblicz opóźnienie, z jakim klocek, któremu nadano pewną prędkość, poruszał się będzie w górę równi pochyłej o kącie nachylenia 30°. Współczynnik tarcia f = 0,1.
Zad 13. Jaka będzie droga hamowania samochodu na asfaltowej nawierzchni, jeżeli typowy czas reakcji kierowcy (czas, jaki upływa od chwili pojawienia się przeszkody do chwili zadziałania hamulców) wynosi 0,7 s, a współczynnik tarcia opon o suchą nawierzchnię asfaltową f = 0,75? Obliczenia przeprowadź dla szybkości samochodu 30 km/h, 60 km/h oraz 120 km/h.
Zad 14. Jaką najmniejszą siłę musimy docisnąć klocek o masie 1 kg do pionowej ściany, aby nie zsunął się w dół? Współczynnik tarcia pomiędzy klockiem a ścianą wynosi 0,2.
Zad 15. Na klocek o masie 10 kg działa siła o wartości 40 N, równoległa do poziomego toru, po którym porusza się klocek. Jaki jest współczynnik tarcia klocka o podłoże, jeżeli porusza się on z przyśpieszeniem równym 2 m/s2?
Dane: m = 10 [kg] F = 40 [N]
a = 2 [m/s2]
Szukane: f = ?































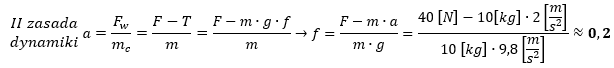
Komentarze
Prześlij komentarz
Chętnie odpowiadamy na każde pytanie oraz podsyłane nam zadania ;)